Verbesserungen mit einer weiteren NaI(Tl)-Sonde

Bild7: NaJ(Tl)-Detektor der holländischen Firma Scionix
Diese Sonde ist sehr gut für Messungen bis mind. 2,5 MeV Photonenenergie nutzbar und ist sehr einfach an den YB-Mini-MCA Vielkanalzähler anschliessbar. Ein Schaltungsbeispiel zeigt das nächste Bild7a
Bild7a: Beispielschaltung, ein NaI-Detektor wird an den YB-Mini-MCA Vielkanalzähler angeschlossen.
Diese Schaltungsvariante ist ausdrücklich nur für den im Bild7 gezeigten Detektor geeignet.
Vorsicht Hochspannung : Die Schaltungsvariante nach Bild7A verwendet ein Hochspannungsmodul von Hamamatsu, welches eine negative Hochspannung gegenüber Batteriemasse erzeugt. Häufig ist die Kathode des Detektors mit dem Detektorgehäuse verbunden. Zwischen Batterie und dem Detektorgehäuse (PMT) kann es deshalb zu einer Hochspannung kommen. Aus Sicherheitsgründen muss in dieser Schaltungsvariante nach Bild7a das Hochspannungsmodul zusammen mit der Batterie in ein separates und schutzisoliertes Gehäuse untergebracht werden. (siehe Schaltung nach Bild7a). Die Photomultipliertube PMT sollte nach Möglichkeit ebenfalls in ein schutzisoliertes Gehäuse gestellt werden. Die Anode des PMT wird über einen Lastwiderstand RL an eine +HV gelegt. Der Lastwiderstand RL=1MOhm, welcher hier mit dem C4900 zusammen im separaten Gehäuse untergebracht ist, darf auf keinen Fall vergessen werden. RL erfüllt auf diese Weise zwei wesentliche Funktionen : 1. Lastwiderstand für die PMT 2.) Hochspannungschutz (Strombegrenzung) im HV-Teil.
Kalibrierpräparate
Wegen dem erweiterten Energiebereich habe ich neben 10g Lu2O3 als weiteres Kalibrierpräparat 290 Gramm KCl eingesetzt, welche in Form einer 8cm durchmessenden Kugel gepresst ist. Der Gammafluss von 290g KCl liegt mit ca. 550 [1/s] in der gleichen Größenordnung mit dem Gammafluss aus dem 10g Lu2O3 Präparat (2x 450 [1/s]). Die Ansprechempfindlichkeit dieser Sonde als Funktion der Photonenenergie lässt sich bis 800keV Photonenenergie anhand der 203keV und 307keV Referenzen des Lu2O3 Präparates und anhand dessen bekanntem Gammafluss näherungsweise berechnen. Oberhalb 800keV bis 3MeV berechnet sich der weitere Verlauf der Funktion anhand der 307keV Referenz des Lu2O3 Präparates und anhand der 1460keV Referenz des KCl- Präparates. Wie ich bei diesen Kalibrierungen vorgegangen bin, habe ich oben am Beispiel eines russischen NaJ(Tl)-Detektors ausführlich beschrieben. Nach den Kalibrierungen habe ich nun weitere Messungen mit dieser Sonde an 60g getrockneten Waldpilzen und 200g Meersalz durchgeführt. Die Spektrogramme dazu sind im folgenden Bild8 zusammengefasst. Es wurden hier die Ergebnisse auf ein Kilogramm Probenmasse umgerechnet.
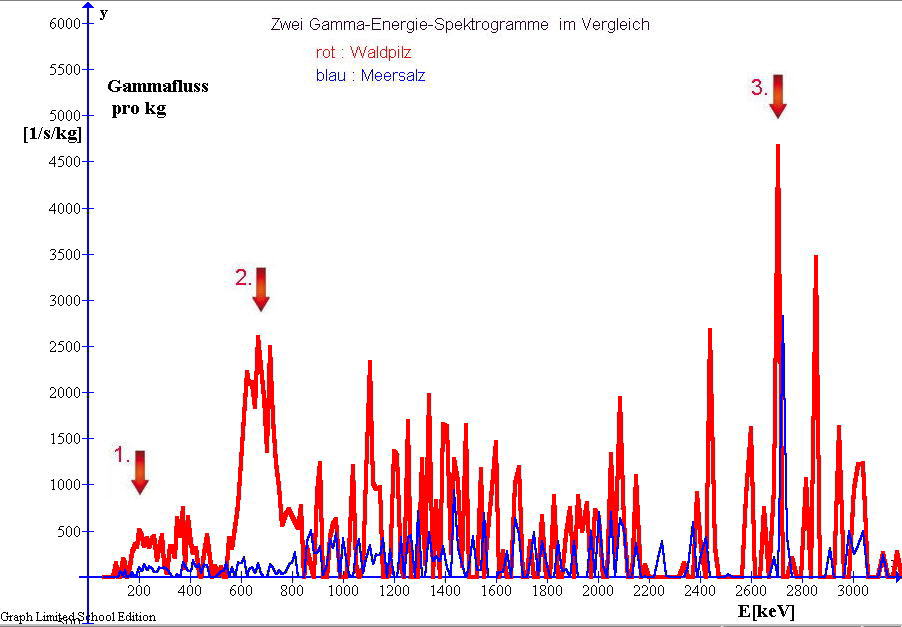
Bild8: gemessenes Gamma-Spektrum von Waldpilzen (rote Kurve)
im Vergleich mit dem gemessenen Spektrum von Meersalz (blaue Kurve);
gemessen mit meinem NaI(Tl) Szintillator
Drei Stellen in diesem Spektrogramm von der Pilzprobe (roter Kurvenzug im Bild8) erscheinen mir besonders auffällig.
Diese habe ich mit Pfeilen markiert:
1.) Abbild von vermutlich mind. 10000 Bq/kg Radium-226 Aktivität
2.) Abbild von möglicherweise (vermutlich) zwischen 1800 Bq/kg bis 3300 Bq/kg Cs-137 Aktivität, sowie möglicherweise hohe Radium-226 Aktivität
3.) Abbild einer weiteren auffälligen Reaktion mit 2600keV bis 2800keV Photonenenergie. Die Reaktion im Photonendetektor zwischen etwa 2600keV Photonenenergie bis 2800keV (siehe Pfeil 3. im Bild8) ist nun auch noch sehr bemerkenswert. Allerdings bin ich mir nicht sicher, ob es sich hierbei um das Abbild eines radioaktiven Nuklids handelt, welches tatsächlich in der Probe enthalten ist, oder ob es sich hierbei um das Abbild einer unerwünschten technischen Nebenreaktion des Messgerätes handelt. Sehr wahrscheinlich handelt es sich hier jedoch um die Abbildung einer Tl-208 Aktivität aus der Zerfallsreihe von Th-232 (E-Gamma=2614.6 keV)
In der Literatur habe ich allerdings auch Informationen über ein Nuklid gefunden, welches beim Zerfall eine Energie von 2750 keV abgibt.[reference] Die Linie im Spektrogramm (Bild8) mit der Markierung 3. könnte demnach auch ein Abbild von Natrium-24 sein. Natrium-24 hat eine kurze Halbwertszeit von nur 15 Stunden. Für eine dauerhafte Präsenz muss es also entweder als Tochternuklid innerhalb einer Zerfallsreihe entstehen, oder durch einen anderen Prozess laufend neu gebildet werden. Mir wurde berichtet, das Natrium-24 durch Neutroneinfang verschiedener Elemente entstehen kann, welche im Fallout von Atomexplosionstests enthalten ist [2]. Dies gibt natürlich entsprechenden Spekulationen Nahrung. Das Spektrogramm von dem Meersalz (blaue Kurve im Bild8) zeigt tatsächlich recht genau an der Stelle 2750keV Photonenenergie das Abbild einer Reaktion in dem eingesetzten Photonendetektor. Nach meiner Interpretation könnte dies auch ein Hinweis auf Rückstände aus Unterwasser-Atomexplosionstests sein.
Aufgrund einem neueren Hinweis aus einem Leserbrief gibt es jedoch inzwischen eine wahrscheinlichere Interpretation . Hiernach handelt es sich nicht um die Abbildung aus Natrium-24, sondern jener einer Tl-208 Aktivität aus der Zerfallsreihe von Th-232 (E-gamma = 2614.6 keV, I-gamma = 35.8%) Bemerkenswert ist, das diese Abbildung in fast allen meinen Spektrogrammen verschiedener Lebensmittelproben in sehr unterschiedlicher Ausprägung erkennbar ist. Neuerdings werte ich die Abbildung der Tl-208 Aktivität aus der Zerfallsreihe von Th-232 mit der Gamma Energie = 2614.6 keV, als eine Indikation für Normstoffe in diesen untersuchten Lebensmittelproben.(vergl. Spektrogramme von Lebensmittelproben )
Wegen meinem Verdacht auf Radium in der Waldpilzprobe habe ich nun das Spektrogramm von einer alten Taschenuhr (radioaktive Leuchtzeiger) mit dem Spektrogramm von einer eingeäscherten Waldpilzprobe verglichen.
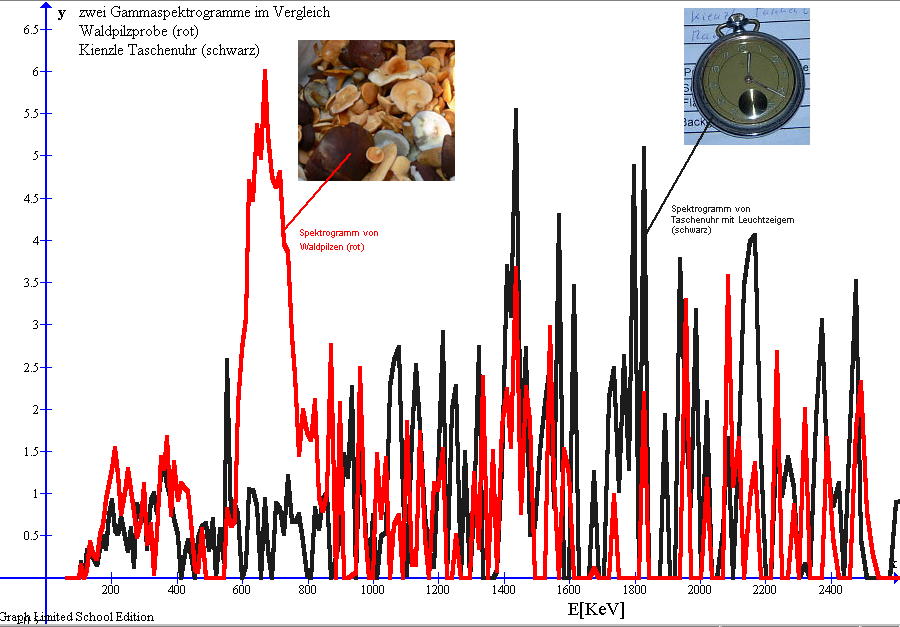
Bild9: Zwei Gamma-Spektrogramme im Vergleich ; Waldpilze und Taschenuhr (radioaktive Leuchtzeiger)
jeweils gemessen mit meinem NaI(Tl)-Detektor
Um einen direkten Vergleich per Augenschein zu ermöglichen, habe ich beide Spektren auf Mittelwert Gammafluss normiert. Neben dem auffälligen Peak (600keV bis 700keV) (ROT) ähnelt das übrige Waldpilz-Spektrogramm durchaus dem gemessenen Spektrum (SCHWARZ) von der Taschenuhr. Übereinstimmungen im Energiebereich unter 500keV erscheinen mir hier besonders auffällig.
Radium ist im Gammaspektrum an den Spektrallinien seiner Zerfallsprodukte (Tochternuklide) erkennbar. Das Maximum (höchster Gammaflluss) im Gammaspektrum von Radium-226 liegt bei ca. 609 keV Photonenenergie. Die entsprechende Spektrallinie ist ein Abbild aus dem Übergang von Bi-214 zu Po-214. Auch in dem gemessenen Spektrum von den Waldpilzen ist der höchste Gammafluss etwa um 600KeV bis 700KeV erkennbar. Es könnte augenscheinlich eine Abbildung aus dem Übergang von Bi-214 zu Po-214 aus der Radium-Zerfallsreihe sein. Weil in den Massenmedien jedoch die Deutung in Pilzproben auf Cäsium-137 mit einer sehr nahe gelegenen Energie bei 660keV betont wird, gehe ich davon aus, das es sich hier um Cäsium-137 handeln könnte, dessen Abbilder aus der Umwandlung sich bemerkbar machen. Allerdings ist mir eine eindeutige Unterscheidung zwischen dem Übergang von Bi-214 aus Radium226 und dem Übergang von Ba137-m aus Cs137 an dieser Stelle wegen der geringen Energieauflösung meines Spektrometers nicht wirklich möglich.
Die folgende Grafik zeigt die mit einer Radium-Quelle und einer Waldpilzprobe und meinem selbstgebauten NaI(Tl)-Spektrometer erzeugten Impulshöhenverteilungen im direkten Vergleich.
Hier mit verlängerter Messzeitspanne für ein genaueres Ergebnis. Energiewerte, die zu den gemessenen Impulshöhen passen , sind auf der Abzisse aufgetragen.
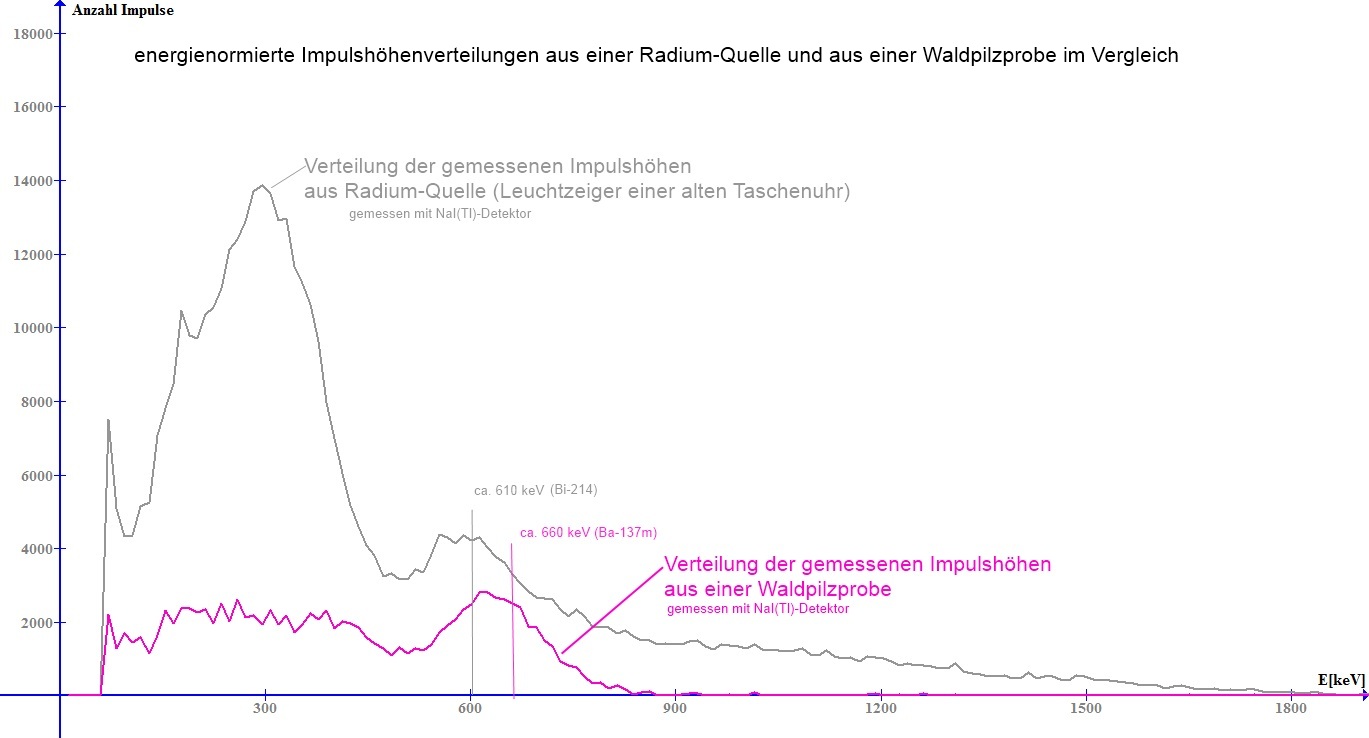
Bild9.1 : Energienormierte Impulshöhenverteilungen im Vergleich.
Erzeugt mit einer Radium-Quelle, einer Waldpilzprobe und meinem NaI(Tl)-Detektor
Im Bild9.1 ist mir anhand der gemessenen Impulshöhenverteilungen ein geringer Unterschied zwischen dem Übergang von Bi-214 aus Radium und dem Übergang von Ba137-m aus Radiocäsium in einem direkten Vergleich erkennbar. Tritt sowohl Radium, als auch Radiocäsium gemeinsam in einer Nuklidmischung auf, dann sind Abbilder, aus der Bi-214 Umwandlung und der Ba-137-m Umwandlung, nicht mehr getrennt erkennbar. Die Impulshöhenverteilung zeigt dann innerhalb des Energiebereich 600keV bis 700keV eine einzige (etwas verbreitete) Anhebung, nämlich die Summe der Abbildungen aus Aktivitäten der Ra-226(Bi-214) und Cs-137(Ba-137-m) Nuklide.
Zum qualitativen Vergleich mit dem gemessenen Spektrum (schwarzer und roter Kurvenzug im Bild9) zeigt das folgende Bild9a ein weitgehend ideales Gammaspektrum aus 100 Bq Radium-226 Aktivität :

Bild9a : Gammaspektrum von Radium-226
(erste fünf große Linien : 186keV U-235 3,28% ; 242keV Pb-214 7,46% ; 295keV Pb-214 19,17% ; 352keV Pb-214 37,06% ; 609keV Bi-214 46,09%)
Der schon nach meinen Untersuchungen mit dem RFT-Szintillator geäußerte Verdacht, das die Waldpilze eine Mischung aus verschiedenen radioaktiven Nukliden enthalten, welches nicht allein mit dem Tschernobyl Reaktorunglück erklärbar ist, sehe ich mit diesen Ergebnissen jedenfalls nachdrücklich bestätigt. Aufgrund der hier besprochenen Auffälligkeiten erscheint es mir ratsam, ein Augenmerk nicht allein nur Cäsium-Aktivitäten zu legen.
Aufteilen der Spektrogramme in Energiebereiche
Ein NaI(Tl)-Detektor hat eine vergleichsweise geringe Energieauflösung. Ein Linienspektrum, so wie in Bild 9a dargestellt, lässt sich mit meinem NaI-Detektor real schwerlich messen. Durch Überlagerungseffekte energetisch benachbarter Ereignisse ist die Unterscheidung benachbarter Spektrallinien erschwert und demzufolge eine eindeutige Nuklididentifizierung mit meinem NaI-Detektor nicht möglich. Um trotz dieser Schwierigkeiten bei der Nuklididentifizierung mit dem NaI-Detektor, Aktivitäten unterschiedlicher Radionuklide messen zu können, teile ich den gesamten interessierenden Energiebereich zwischen 100keV bis 2,5MeV, entsprechend der Energieauflösung des Detektors, in mehrere weit gestreckte Energiebereiche auf. Eine Bestimmung der Aktivität einzelner Nuklide wird hierbei nicht angestrebt. Stattdessen wird mittels sog. Leitnuklide ein Maßstab für die "wahrscheinliche Aktivität" (Aw) innerhalb dieser Energiebereiche konstruiert (siehe dazu auch: "Spezifische Aktivität abschätzen").
Beobachtete Energiebereiche und deren Trennung in Stoffgruppen
Tabelle1a
| Nr. | Energiebereich | Bezeichnung (Stoffgruppe) |
| 1.) | 100keV bis 620keV | NORM (Ra-226) |
| 2.) | 620keV bis 700keV | Cs137 |
| 3.) | 700keV bis 2,5MeV | sonstige |
Für Materialproben mit hohem Kaliumgehalt zusätzlich :
Tabelle1b
| Nr. | Energiebereich | Bezeichnung (Stoffgruppe) |
| 4. | 1400keV bis 1520keV | K40 |
Weitere Informationen zur Kalibrierung
Gammafluss (Gamma-Emission) abschätzen :
Gemessene Spektrogramme teile ich in verschiedene Energie-Bereiche ein (siehe Tabelle1a und Tabelle1b). Für jeden dieser Energiebereiche soll separat der Gammafluss abgeschätzt werden, welcher in den jeweiligen Energiebereich fällt und über die Oberfläche des Probenbehälters (Plexiglaskugel mit 8cm Durchmesser) fließt.
Um eine Umrechnung auf die spezifische Aktivität vorzubereiten wird der Messwert für diesen Gammafluss auf die in den Probenbehälter eingefüllte Probenmasse bezogen und auf 1Kg Probenmasse umgerechnet. Analog zu "spezifische Aktivität" nenne ich das Ergebnis "spezifischer Gammafluss" bzw. "Gammafluss pro Kilogramm". ( Auch "spezifische Gamma-Emission" bzw. "Gamma-Emission pro Kilogramm" ) wobei der Ausdruck "Gamma-Emission" , sofern auf eine Masse bezogen wird, die meinem Gefühl nach konsequentere Bezeichnung wäre, wärend der Ausdruck "spezifischer Gammafluss" sich auf eine Oberfläche bezieht. . Weil jedoch die einfliessende Gamma-Emission in der Regel vollständig über eine begrenzende Oberfläche abfliesst, verwende ich die Begriffe "Gamma-Emission" und "Gammafluss" gern synonym.
Zur Berechnung der spezifischen Gamma-Emission (spezifischer Gammafluss) werden die numerischen Werte signifikanter Abbilder (Spektrallinien) über den jeweiligen Energiebereichen summiert bzw. integriert und das Ergebnis wird mit einem Kalibrierfaktor bewertet. Als Kriterium für eine Signifikanz gelte hierbei die Überschreitung der Zwei-Sigma-Grenze. In den jüngsten Spektrogrammen habe ich signifikante Abbilder mit dicken roten Linien hervorgehoben. Nicht signifikante Abbilder sind in meinen jüngsten Spektrogrammen mit dünner roter Linie gezeichnet. Ein Beispiel zeigt Bild10:
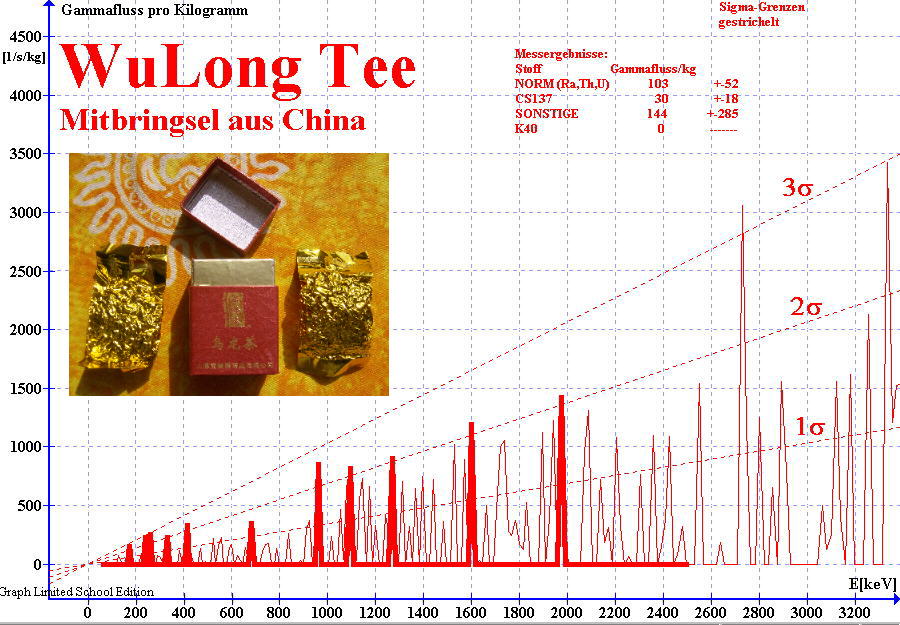
Bild10: Gammaspektrogramm einer Teeprobe
Abschätzen der zufälligen Messfehler :
| Was
ist gemeint mit "Zwei-Sigma-Grenze" Beim radioaktiven Zerfall ist nicht vorhersehbar, welches Atom wann zerfallen wird. Es handelt sich um einen sog. statistischen Prozess. Grundlage zur Berechnung des zufälligen Messfehlers bietet hier eine Theorie der Verteilung nach Poisson. Die Poissonverteilung kann hierbei häufig durch eine Standardverteilung angenähert werden. Diese Theorie kann auch auf Zählergebnisse angewendet werden, welche eine Messapparatur (Szintillator, Photomultiplier ,MCA, PC) aus Effekten ionisierender Strahlungen liefert und auf ein Spektrogramm abbildet. Bei der Beurteilung ob eine bestimmte Abbildung (Spektrallinie) im Spektrogramm signifikant ist (also nicht nur aus zufälligen Messfehlern entstanden ist) , erscheint mir die Berechnung von sog. Sigma-Grenzen hilfreich. In der Messtechnik
wird häufig eine Normalverteilung angesetzt, welche die
Streuung
der
zufälligen Messfehler beschreibt. Hierbei ist von Bedeutung,
ob
das Messergebniss ausserhalb einer gewissen Streubreite
(Grenze)
fällt. Fällt es ausserhalb einer gewissen Grenze,
dann ist es
von Bedeutung, denn es wird mit grosser Wahrscheinlichkeit nicht nur
ein Abbild von zufälligen Messfehlern sein. W > Nσ <==> W ist signifikant ==> Die Aktivität in der Probe ist verschieden von Null (Die Materialprobe ist aktiv) (mit anderen Worten: W > Nσ <==> W ist von Bedeutung ==> DieAktivität in der Probe ist verschieden von Null). Für den anderen Fall : W < Nσ <==> W ist nichtsignifikant <==> Die Aktivität in der Probe ist unbestimmt (mit anderen Worten: W < Nσ <==> W ist möglicherweise von Bedeutung <==> Die Aktivität in der Porbe ist unbestimmt) Im Gamma-Spektrogramm ergibt sich die Sigma-Grenze σ jeder einzelnen Abbildung näherungsweise aus der Differenzierung ihrer mathematischen Formulierung und anschließendes Einsetzen der zufälligen Messfehler (Quadartwurzel der Zählerstände). Differenziert wird entsprechend dem Fehlerfortpflanzungsgesetz (Fehlerrechnung). Im rektifizierten Gamma-Spektrogramm wird die Abbildung zweier Zählerstände durch eine Funktion beschrieben deren Ableitungen entsprechend dem Fehlerfortpflanzungsgesetz numerisch per Computernäherungsweise berechnenbar ist. Es hat sich gezeigt , das der Verlauf der auf diese Weise berechneten sigma-Grenze im rektifizierten Gamma-Spektrogramm, welches ich mit meinem NaI(Tl)-Detektor gemessen habe, etwa einer Geraden durch den Ursprung folgt. Deshalb stelle ich den Verlauf der sigma-Grenzen (σ1 = σ ; σ2 = 2σ) im rektifizierten Spektrogramm vereinfacht als Geraden durch den Ursprung dar. Zur Verdeutlichung der grundliegenden Rechnung dient folgendes Beispiel anhand zwei Messungen mit dem Geiger-Müller-Zähler : Es sind zwei unabhängige Impuls-Messungen mit einem Geigerzähler vorgenommen worden. Der erste Messwert sei die Anzahl der gezählten Impulse X1 = 790 für die Probe und der zweite Messwert sei X2 =625 für Backgr. Es ist nun anhand dieser beiden Messwerte zu prüfen ob die Probe frei von Radioaktivität ist. Die Messwerte sind grösser 50 also kann die Poissonverteilung durch Normalverteilung angenähert werden und nun rechnet sich wie folgt : Erste Messung : 1.) X1= 790 sei der Messwert einer Zufallsvariablen. Die ZV ist normalverteilt mit N(u1,s1^2) ; s1=Wurzel(X1)=28 Zweite Messung : 2.) X2 = 525 sei der Messwert einer weiteren Zufallswariablen. Die ZV ist normalverteilt mit N(u2,s2^2) ; s2=Wurzel(X2)=23 Beide Messungen sind unabhängig voneinander. Als Mass (Messergebnis) für die in der Materialprobe enthaltene Aktivität wird nun eine Differenz "Zufallsvariable X3" gebildet: Rechnerisch ergibt sich: X3:=X1-X2 = 790-525 =265 . Diese zugrundlegende Zufallsvariable X3 ist nun wieder normalverteilt (Faltungsinvarianz der Normalverteilung) allerdings mit N(u3,s3^2)=N(u1-u2,s1^2+s2^2). Damit ist: σ = s3 = Wurzel(28^2+23^2) = 36 und es gilt wegen Annäherung der ZV X1 und ZV X2 an die Poissonverteilung natürlich auch: I. σ = s3 = Wurzel(X1+X2) = Wurzel(790+525) = 36 WEITERES (Herleitung von I. nach dem Fehlerfortpflanzungsgesetz) Einfacher Sigma-Test: Für den Test auf Signifikanz wird nun abgefragt ob das Messergebnis X3=265 grösser einer bestimmten Sigma-Grenze G ist. Als die bestimmte Sigma-Grenze gelte hier Beispielhaft die Erkenungsgrenze (Zwei-Sigma-Grenze) G=2σ : Das Rechenbeispiel liefert: X3= 265 σ =36 2σ =72 und in diesem Beispiel ist X3 > 2σ ==> X3 ist signifikant ==> Die Materialprobe ist aktiv Weitere Leermessungen als ergänzende Methode zur Abschätzung zufälliger Messfehler: Berechnungen der Sigma-Grenzen erfordert etwas mathematisches Hintergrundwissen. Eine andere praktikabele Methode, zufällige Messfehler abzuschätzen bieten sog. weitere Leermessungen. Hierzu wird die Messung an der Probe durch eine weitere Leermessung ersetzt. Dann wird das Ergebniss (Differenz) aus zwei Leermessungen analog dem Ergebnis aus der Probenmessung abgebildet. Auf diese Weise entstehen Abbilder von zufälligen Messfehlern. Die Abbilder zufälliger Messfehler aus Leermessugen entsprechen im Spektrogramm näherungsweise dem Verlauf von Sigma-Grenzen. Error-Level : Wird die Differenz aus den Messergebnissen der Probe abzüglich der Messergebnisse aus der Leermessung (Nulleffekt bzw. Gamma-Hintergrund) auf ein Spektrogramm abgebildet, dann treten viele Abbilder mit Werten kleiner Null (negative Abbilder) in Erscheinung. Beträge dieser Abbilder, markieren den Verlauf des Error-Level. Das 1,4-fache (Wurzel2-fache) des Error-Level entspricht näherungsweise dem Verlauf der Ein-Sigma-Grenze. |
Kalibrierfaktoren werden anhand Vergleichsmessungen mit Kalibrierpräparaten so gewählt, das Messergebnisse welche sich durch Messungen an den Kalibrierpräparaten ergeben, hinreichend mit der Erwartung übereinstimmen. Die hier zur Kalibrierung verwendeten Präparate und deren Erwartungswerte (spezifischer Gammafluss und spezifische Aktivität) sind :
Tabelle2:
| Präparat | Energiebereich | Gammafluss/kg [1/s/kg] |
Spezifische Aktivität [Bq/kg] |
| Lu2O3 | 100keV-400keV | 90000 | 45000 |
| KCl | 1400keV-1520keV | 1800 | 18000 |
Bewertung der Messergebnisse über den gesamten genutzten Energiebereich (100keV bis 2,5MeV) geschieht mittels Approximation des für NaI(Tl)-Detektoren charakteristischen Ansprechvermögens [5]. (Vergleiche auch oben auf dieser Seite : Effektivitäts-Kalibrierung des russischen NaI(Tl)-Detektors)
Spezifische Aktivität abschätzen :
Zur Umrechnung des gemessenen Gammafluss/kg in eine spezifische Aktivität wird ein Nuklid ausgewählt, dessen Abbilder in einem beobachteten Energiebereich erwartet werden und für die betreffende Stoffgruppe als charakteristisch gelten darf. Dieses Nuklid gilt als sog. "Leitnuklid" mit seinen Strahleneigenschaften dann als Vertreter für die gesamte Stoffgruppe.
Die Umrechnungen der in den Stoffproben gemessenen spezifischen Gammaflüsse in die spezifischen Aktivitäten orientiert sich an den Strahleneigenschaften von ausgewählten Leitnukliden. Da ich vornehmlich Messungen in Lebensmittelproben durchführen möchte, fällt die Auswahl auf solche Radionuklide, von welchen mir bekannt ist, das diese in Lebensmittel hineingeraten. Überdeckt das Leitnuklid mit seiner Wirkung andere schwächer strahlende Radionuklide welche mit ihrer Strahlung ebenfalls in dem beobachteten Energiebereich präsent sind, dann wird die Umrechnung des gemessenen spezifischen Gammafluss in eine spezifische Aktivität sinnvoll durch Multiplikation mit einem Multiplikationsfaktor. Dieser Multiplikationsfaktor ist durch den höchsten Gamma-Anteil in der Zerfallsreihe des Leitnuklid (incls. Tochternuklide) reziprok bestimmt. Das auf diese Weise ermittelte Messergebnis nenne ich die spezifische wahrscheinliche Aktivität (spez. Aw) .
Wesentliche Daten und Informationen, welche ich für die Interpretation meiner gammaspektrometrischen Messergebnisse in Lebensmittelproben heranziehe, sind in den folgenden Tabelle3 und Tabelle4 zusammengefasst :
Tabelle3:
| Bezeichnung Stoffgruppe |
Energiebereich |
Leitnuklid (Indikator) |
Gamma- Anteil [%] |
Multiplikationsfaktor zur Umrechnung des Gammafluss/kg in die spezifische Aktivität |
| NORM (Ra,U,Th) | 100keV - 620keV | Radium-226 (Bi-214) |
46 | 2 |
| CS137 | 600keV - 700keV | Cäsium-137 (Ba-137m) |
90 | 1,1 |
| Sonstige | 700keV - 2,5MeV | nicht angegeben | 50 | 2 |
| Sonstige | 700keV *
-1400kev und 1520keV- 2,5MeV |
nicht angegeben | 50 | 2 |
| K40 | 1400keV - 1520keV |
Kalium-40 | 10 | 10 |
Tabelle4:
Tabelle4: Gamma-Energieen und Emissinswahrscheinlichkeiten einiger natürlicher und künstlicher Radionuklide [Referenz]
Was ist gemeint mit "NORM" : Im Dezember 2009 wurde der Öffentlichkeit bekannt, dass bei der Erdöl- und Erdgasförderung jährlich Millionen Tonnen radioaktiv verseuchter Rückstände anfallen, für dessen Entsorgung größtenteils der Nachweis fehlt.[reference] Im Rahmen der Förderung an die Erdoberfläche gepumpte Schlämme und Abwässer enthalten NORM-Stoffe (Naturally occurring radioactive material), u. a. das hochgiftige und extrem langlebige Radium226 (Ra-226) sowie Polonium210. Es wurde bekannt, das diese hochgiftigen radioaktiven Abfälle durch ungesonderte industrielle Entsorgung sich über der Erdoberfläche anreichern und in die Nahrungskette gelangen. Was ist gemeint mit "Cäsium-137" : Das radioaktive Isotop Cäsium-137 , ein Produkt der Kernspaltung, fand in der Öffentlichkeit besondere Beachtung, als es infolge der Katastrophe von Tschernobyl am 26. April 1986 in größeren Mengen in die Umwelt gelangte. Cäsiumnuklide werden als Indikatoren für unnatürliche Strahlung herangezogen. Was ist gemeint mit "Kalium-40" * Erläuterung ; warum ist die radioaktive Strahlung aus Kalium für Organismen unschädlich: Kalium ist an der Erdoberfläche schon immer weit verbreitet. Zwar schädigt die radioaktive Strahlung aus Kalium den Organismus auch., jedoch haben Organismen besonders auf Kalium abgestimmte Reperaturmechanismen entwickelt. Auch besitzt jeder Organismus einen sog. Kaliumhaushalt, überschüssiges Kalium wird umgehend aus dem Körper ausgeschieden. |
Kurzbeschreibung
Entstehung und Berechnung des Gamma-Spektrogramms
Auf erforderliche Kalibrierungen des Messgerätes gehe ich hier nicht näher ein. Ausführliche Beschreibungen dazu finden sich auf den vorangegangenen Seiten.
Sofern ich ein Gammaspektrum aus Messdaten erzeugt habe, schreibe ich in der Regel "Gamma-Spektrogramm" anstelle von "Gammaspektrum". Eine solche Differenzierung in der Bezeichnung ist in der von mir gesichteten Literatur unüblich. Jedoch möchte ich mit dieser Differenzierung einer Gleichwertung, meiner mit einem NaJ-Detektor gemessenen Gammaspektren, mit idealen theoretisch erwarteten Linienspektren vorbeugen.
Nun jedoch zur Beschreibung:
Im Bild11 habe ich die Entstehung des Gamma-Spektrogramms anhand mehrerer Einzelbilder dargestellt.
Das Gamma-Spektrogramm entsteht aus zwei Impulshöhenspektren (Rohdaten). Dazu werden zunächst die grundliegenden Impulse mittels einer Messanordnung aus Probenbehälter mit Probe, Szintillator und Photomultiplier erzeugt und die Impulshöhen werden mit einem MCA gemessen. Der MCA überträgt online alle Messwerte digitalisiert an einen PC. Dort werden diese digitalisierten Daten auf einem Speicherplatz der PC-Festplatte abgelegt. Nach dem Messvorgang liest ein PC-Programm offline die digitalisierten Werte aller gemessenen Impulshöhen von der Datei und sortiert diese in 256 Zähler (Kanäle) zu einem Impulshöhenspektrum. Dieses Impulshöhenspektrum wird daraufhin in das Gamma-Spektrogramm transformiert (abgebildet).
Es sind grundsätzlich zwei Messvorgänge erforderlich. Der erste Messvorgang geschieht mit einem leeren Messbehälter (Leermessung). Hierbei entsteht ein Impulshöhenspektrum in welchem die Aktivität des Background abgebildet ist. Im zweiten Messvorgang ist der Messbehälter mit einem Probenmaterial gefüllt. Es entsteht ein Impulshöhenspektrum, in welchem die Aktivität des Background und die Aktivität der Materialprobe abgebildet ist. Die rechnerische Subtraktion (viertuelle Bleiburg) eliminiert Abbilder von Aktivitäten aus dem Background.
Daten welche während dieser ersten beiden grundliegenden Messvorgänge entstehen, können durch rechnerische Subtraktion des Backgroundspektrums theoretisch auf ein Impulshöhenspektrum abgebildet werden, welches dann nur noch Abbildungen von Aktivitäten aus der Materialprobe enthält. Durch geeignete Transformation lässt sich dieses Impulshöhenspektrum rektifizieren und auf ein Gamma-Spektrogramm (gemessenes Gamma-Spektrum) abbilden. Das Bild11 zeigt dazu beispielhafte Ergebnisse.
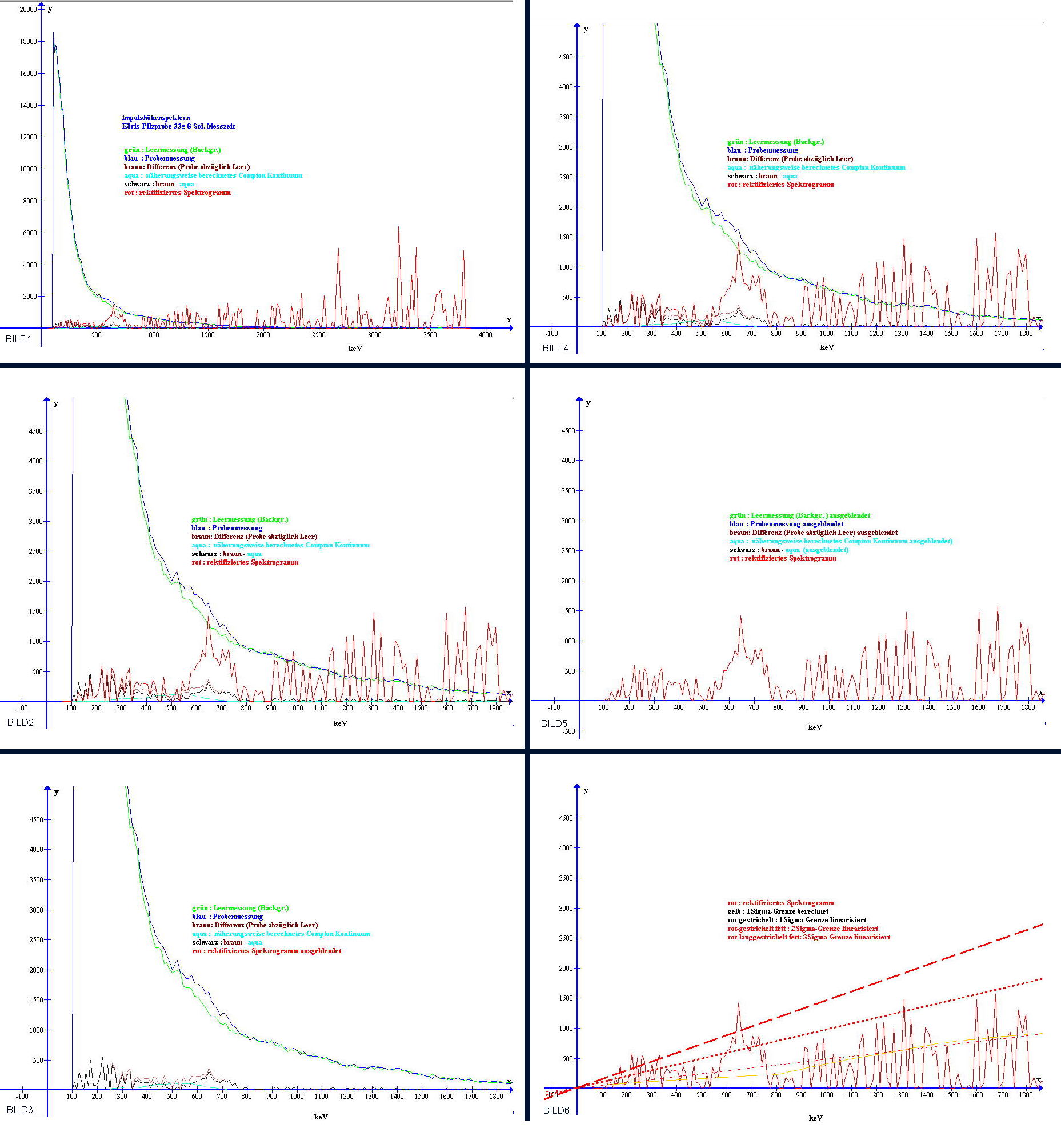
Bild11: Entstehung des Gamma-Spektrogramms
Im Bild11 sind Impulshöhenspektren (Bild11 oben links) von einer Waldpilzprobe dargestellt. Das grundliegende Impulshöhenspektrum von der Messung ohne Probe (Leermessung bzw. Backgr.) ist mit grüner Farbe gezeichnet. Das grundliegende Impulshöhenspektrum, welches durch Messung an dem mit der Materialprobe gefüllten Behälter entstanden ist, wurde im Bild mit blauer Farbe eingezeichnet. Im nächsten Rechenschritt wird die Differenz dieser beiden grundliegenden Impulshöhenspektren gebildet (viertuelle Bleiburg). Das Ergebnis ist unten links im Bild11 als braune Kurve erkennbar. In einem weiteren Rechenschritt wird das näherungsweise Compton-Kontinuum (hellblaue Kurve) berechnet und ebenfalls subtrahiert. Auf diese Weise entsteht die in den Bildern (Bild11) schwarz gefärbte Darstellung eines Impulshöhenspektrums, in welchem nun sowohl der Leereffekt, als auch Effekte aus Streuereignissen (näherungsweise berechnetes Compton-Kontinuum) eliminiert ist.
Wegen der energieabhängigen Effizienz des Szintillators erscheinen die grundliegenden Impulshöhenspektren im Vergleich zu einem Gammaspektrum verzerrt. Um einen Gammafluss über einen weitreichenden Photonenenergiebereich unverzerrt darzustellen zu können, wird nun eine Transformation gerechnet, welche das Impulshöhenspektrum auf das Gamma-Spektrogramm abbildet (rektifiziert). Dazu wird das Impulshöhenspektrum in welchem sowohl der Leereffekt, als auch Effekte aus Streuereignissen schon eliminiert sind, auf die Funktion eff(E) bezogen. Die Funktion eff(E) ist aus einer Effektivitätskalibrierung hervorgegangen, welche zuvor mittels geeigneter Kalibrierpräparate durchgeführt wurde. (Eine Beschreibung zur Effektivitätskalibrierung finden Sie auf der vorangegangenen Seite). Die Effektivitätskalibrierung unter 100keV ist wegen verschiedener physikalischer Effekte nicht trivial, deshalb habe ich Werte unterhalb 100keV Photonenenergie dafür nicht berücksichtigt.
Nun ist das Impulshöhenspektrum auf die Funktion eff(E) bezogen und das Ergebnis ist im roten Kurvenzug dargestellt (Bild11, rechts Oben und rechts Mitte).
Im Bild11 rechts Unten ist auch ein expliziter Verlauf von der Ein-Sigma-Grenze (gelb) eingezeichnet. Es ist erkennbar, das diese näherungsweise einer Geraden durch den Ursprung folgt.
Eine weitere Vergleichsmöglichkeit bietet die folgende Dokumentation eines Spektrogramms von Pottasche, welche ich im 1 Kg Beutel als Gewürz E501 von einem Onlinegewürzhändler bezogen habe. 300g davon habe ich zu einer Kugel mit 8cm Durchmesser geformt und in der gleichen Messanordnung und gleicher Vorgehensweise, wie am Beispiel der Pfifferlinge gemessen.
Die grundliegenden gemessenen Impulshöhenspektren dazu zeigt das folgende Bild:
Bild13 : 300g Pottasche ;grundliegendes Impulshöhenspektrum (Rohdaten)
gemessen mit NaJ(TI) Detektor
Als Ergebnis nach der Datenaufbereitung mit meiner aktuellen Software entsteht das Gamma-Spektrogramm wie folgt :
Pottasche Handel Deutschland Oktober 2011;
Messergebnisse :
Energiebereich Gammafluss/kg spez. Aw
von-bis [keV] [1/s/kg] Bq/kg]
100-620 190 380 u.d.N
600-700 7 8 u.d.N.
700-2500 1212 2424 *
1400-1520 2091 20910 *
Gesamt: 3500 23722
Gut erkennbar ist der K40-Peak um 1460keV. Meine selbst gebastelte Software berechnet die wahrscheinliche spezifische Aktivität (spez.Aw) im Energiebereich zwischen 1400 keV bis 1520 keV in der Pottasche aus den gemessenen Daten zu 20910 Bq/kg (siehe *) . Den Erwartungswert anhand des Kaliumgehaltes in der Pottasche nehme ich mit etwa 16000 Bq/kg bis 18000 Bq/kg an. Für meinen Hausgebrauch bin ich mit 20910 Bq/kg als Messergebnis zufrieden. Das Messergebnis kommt dem Erwartungswert recht nahe und liegt auf der sicheren Seite (ist nicht zu niedrig abgeschätzt).
Es fällt mir allerdings auf, das im Spektrogramm Abbildungen aus Ereignissen zwischen etwa 1000keV bis 1200keV erkennbar sind, welche von meiner Software mit 2424Bq/kg (siehe *) (Sonstige Aktivitäten im Energiebereich 700 keV bis 2500 keV) automatisch veranschlagt werden. Möglicherweise handelt es sich an dieser Stelle um residuale Abbilder aus Streuereignissen (Compton-Spektrum). Das Compton-Spektrum sollte vollständig aus dem Spektrogramm eliminiert werden. Tatsächlich wird es näherungsweise eliminiert. So bald wie möglich möchte ich diesen Versuch mit chemisch reinstem Kaliumchlorid wiederholen um (falls erforderlich) die Datenaufbereitung und Auswertung zu verbessern.
Inzwischen habe ich mit meinem Eigenbau Gamma-Spektrometer auch eine 300g Probe
Kaliumchlorid reinst untersucht. Das Spektrogramm sieht erwartungsgemäss dem Spektrogramm von den 300g Pottasche sehr ähnlich.
Kaliumchlorid reinst Ph.Eur.,USP
Handel Deutschland Oktober 2011;
Messergebnisse :
Energiebereich Gammafluss/kg spez. Aw
von-bis [keV] [1/s/kg] Bq/kg]
100-620 94 188 u.d.N
600-700 13 14 u.d.N.
700-2500 1024 2048
1400-1520 1910 19100
Gesamt: 3041 21350
Gut erkennbar ist der Peak um 1460kev und auch die numerischen Messergebnisse finde ich für meinen Hausgebrauch ganz brauchbar. Wieder erscheint jedoch eine kleinere Anhebung im Spektrogramm zwischen 1000keV bis 1200keV. Vermutlich treten hier noch Reste aus einem nicht vollständig eliminierten Compton Spektrum in Erscheinung. Na Ok meine Auswertesoftware ist noch verbesserungsfähig. Nun kommen in anderen Lebensmitteln glücklicherweise keine so hohen Kaliumkonzentrationen vor, wie in Pottasche (Backtriebmittel, Backpulver) und Kaliumchlorid (Diätsalz). Residuale Abbildungen in den Spektrogrammen, aller anderer von mir bisher untersuchter Lebensmittel, halte ich deshalb an dieser Stelle und in Bezug auf die Genauigkeit des Messergebniss noch für vernachlässigbar. Eine verbesserte Elimination residualer Abbildungen aus Streuereignissen, welche in meinen Spektrogrammen in dieser Versuchsanordnung und aus Lebensmittelproben mit sehr hohen spezifischen Aktivitäten (über einige tausend Bq/kg) entstehen, könnte dann eine Bastelaufgabe für mich darstellen....vielleicht eine Bastelaufgabe für kalte und verregnete Winterabende ? Mal schauen was mir dazu noch schönes und brauchbares einfällt
Fortsetzung folgt.....