Wachstumskomponente                                                                                                  08.01.2008
Definition und numerische Berechnung

Gegeben sei eine Funktion z=f(t) .
Die Wachstumsfunktion W(t) der Funktion z wird durch eine Annäherung berechnet, welche sich aus der Methode der kleinsten Quadrate ergibt.

Hierbei wird von mir eine Näherungsfunktion w=a*t+b als Wachstumskomponente bezeichnet, für welche die Größe

M= INTEGRAL [log(z)-w)]² dt  

den kleinsten Wert annimmt.

Durch die Forderung, dass die partiellen Ableitungen von M nach den Parametern a und b der Funktion w  verschwindet ergeben sich Gleichungen , welche es gestatten die Parameter a und b der Wachstumskomponente w zu ermitteln. Hierbei ist der Parameter a der Wachstumskomponente gleich dem numerischen Wert für die "mittlere Zuwachsrate".

Aus diesen Definitionen ergibt sich für W(t) eine Exponentialfunktion als Wachstumsfunktion und für w eine Geradengleichung als Wachstumskomponente mit den Parametern a und b.
 
Weitere Erläuterungen mit numerischem Rechenbeispiel :

Als numerisches Rechenbeispiel sei eine diskrete Messwerte Reihe mit einer endlichen Anzahl Elementen.vorgegeben.
Jedes Element sei gegeben durch ein Wertepaar (t,z)
t gibt eine numerische Beschreibung des Zeitpunktes der Messung (Zeitvariable).
z quantifiziere den im Zeitpunkt t ermittelten Messwert.
Z  sei die zu z gehörige Messgrösse mit der physikalischen Einheit {z}.

Zur Verdeutlichung sollen hier fünf Messwertepaare einer Messwertereihe radioaktiver Strahlen-Messwerte dienen.

Es gelte :
Z  sei eine Messgröße , deren numerischer Wert auf der Skala eines Messgerätes für radioaktive Strahlung abgelesen wird.
{z} sei die Einheit von Z 
t   sei eine numerische Angabe für den Ablesezeitpunkt von Z
z  sei der numerische Wert der auf ihre Einheit normierten Messgröße  
n die Anzahl der Messwertepaare

Ein Rechenbeispiel gibt folgende Tabelle aus fünf  Wertepaaren:
Tabelle 1
:
 t     z 
0     22000
1     22300
2     22500
3     22550
4     22600

Rektifiziert: werden t und y=ln z
woraus sich Tabelle 2 ergibt
Tabelle 2
:
t     y
0     9.998
1    10.012
2    10.021
3    10.023
4    10.026

nun wird die lineare Annährung  (Regressionsgerade) nach der bekannten Methode der kleinsten Quadrate nach Gauß berechnet.

Unter Verwendung der von Carl Friedrich Gauß eingeführten Schreibweise

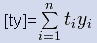( analoge Bedeutung für  : [y] [t] [tt] )  

lautet die Bestimmungsgleichung für a:

I .     a= ([ty]/n-([t][y]/n/n))/([tt]/n-[t][t]/n/n)

und die Bestimmungsgleichung für b :
II.     b= [y]/n-a[t]/n

in unserem numerischen Rechen-Beispiel berechnet sich:

[t]= 10
[y]=50.08
[tt]=30
[ty]=100.23
n=5

aus diesen Werten ergibt sich anhand der Bestimmungsgleichung I. die mittlere Zuwachsrate a zu:

a=0.007
======

Dieses Ergebnis entspricht  :  a= 0,7%. mittlere Zuwachsrate.

In analoger Weise wende ich die beschriebene Vorgehensweise auf Messwerte-Reihen mit weitaus größerer Anzahl Wertepaare an. Alle numerischen Berechnungen hierzu werden mit einer Maschine durchgeführt, welche nach den Grundlagen von John von Neumann funktioniert.


Berechnung der Parameter a und b der Wachstumskomponente
Ein Beispiel für ein C-Programm


----------------------------------------------------------------------------------------------
HOME         IMPRESSUM

(letzte Textänderung 13.01.2008)